Introduction
La manière la plus simple d'effectuer un calcul des incertitudes, c'est d'utiliser la méthode min-max.
On peut aussi utiliser la règle que l'incertitude absolue sur la somme (ou la différence) de deux grandeurs est égale à la somme des incertitudes absolues sur chacune des grandeurs et que l'incertitude relative sur un produit (ou un quotient) est donnée par la somme des incertitudes relatives sur chaque terme.
Il existe également une manière plus compliquée, basée sur des dérivées partielles de la fonction utilisée pour calculer un résultat (voir plus bas).
Le programme en question utilise (implicitement) cette dernière méthode, mais son utilisation est on ne peut plus simple :
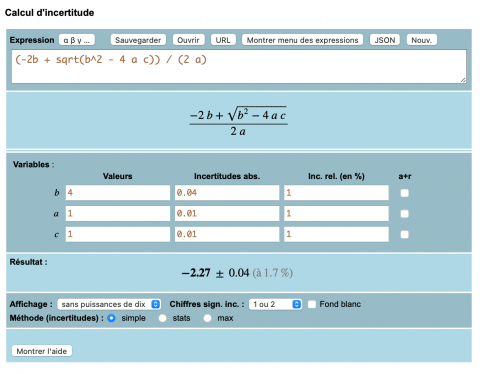
- Introduire une formule dans la rubrique Expression (par exemple : B = sqrt(2 m U / e) / r). Attention d'espacer le variables !
- Contrôler que la formule mise en forme (apparaissant sous l'expression) correspond bien à celle qu'on voulait…
- Donner une valeur à chaque variable (qui peut être une constante) ainsi que son incertitude (absolue ou relative)
- Lire le résultat dans la rubrique Résultat…
A quoi bon ?
Voici quelques arguments pour l'utilisation d'un programme calculant les incertitudes à la place de l'élève :
- Les calculs ne sont pas toujours des sommes et des produits, mais peuvent comprendre des racines ou des fonctions trigonométriques et avec certaines formules, le calcul devient vite compliqué…
- Ces calculs sont souvent fastidieux et si un compte-rendu de TP est demandé à la fin des deux périodes, le temps est compté…
- Le fait de voir l'expression mise en forme permet d'éviter des fautes de calcul !
- Même si le calcul se fait automatiquement, l'étape (à mon avis très importante) consistant à estimer les incertitudes sur les grandeurs mesurées ne peut être sautée (en fait si car au moment de la création de la ligne pour une certaine grandeur, la valeur vaut toujours 1 et l'incertitude absolue 0.01 :-)
- Accessoirement, le programme m'a souvent permis d'entrer une formule pour le résultat d'une question de test de physique, puis de varier les paramètres (valeurs des variables) jusqu'à ce que le résultat soit plausible (le calcul des incertitudes étant alors secondaire)…
Quelques commentaires
L'aide de l'application (bouton tout en bas de l'écran) donne une explication pour la plupart des boutons et menus de l'application ainsi que quelques conseils. Voici quelques extraits :
Calcul des incertitudes
Pour calculer l'incertitude absolue sur le résultat, on utilise la formule avec les dérivées partielles simplifiée (méthode simple, f étant la fonction donnant le résultat en fonction de n variables x1 à xn) :
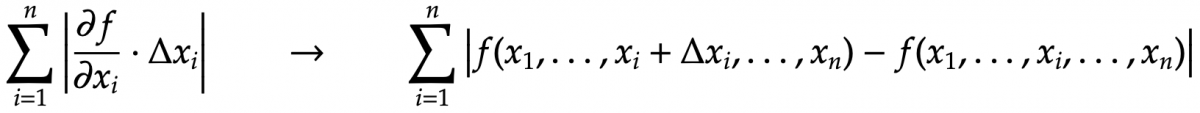
Avec la méthode mieux, on utilise la formule suivante, censée mieux tenir compte des statistiques (mais est-elle vraiment applicable ?) :
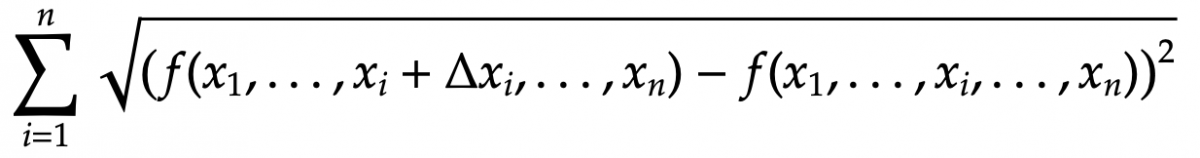
La troisième méthode (max), reprend la première, mais fait varier l'incertitude sur chaque variable entre +(inc. abs) et -(inc. abs), de manière indépendante. Par exemple, si on a 3 variables et qu'on choisit 7 valeurs différentes pour chaque variable, le programme calculera donc 7·7·7 = 343 résultats différents et prendra le plus positif pour l'incertitude positive et le plus négatif pour l'incertitude négative. Cette méthode est avantageuse si la fonction f est hautement non linéaire et si les incertitudes sont grandes. De même, pour des fonctions qui ont un ensemble de définition limité (par exemple asin() ou sqrt(), tous les résultats donnant une valeur impossible (NaN) seront écartés.
Incertitudes absolues ou relatives ?
On peut modifier soit l'incertitude absolue, soit l'incertitude relative pour une variable donnée, l'autre étant recalculée automatiquement, sauf si la case a+r est cochée car dans ce cas la somme deux est utilisée dans le calcul (utile pour des instruments comme des voltmètres qui ont une incertitude absolue pour la position du zéro et une incertitudes relative pour l'étalonnage)…
Arrondis
Pour arrondir le résultat, le programme arrondit d'abord l'incertitude absolue sur le résultat à 1 ou 2 chiffres significatifs (1 chiffre si le premier chiffre est supérieur à 1 et à 2 chiffres sinon…), puis il arrondit le résultat de manière à avoir le même nombre de chiffres avant ou après la virgule (la puissance de dix étant toujour la même pour le résultat et l'incertitude, quelle que soit le choix de l'affichage (voir ci-dessous). Par contre, on peut choisir un nombre de chiffres significatifs plus élevé et on peut également supprimer l'affichage de l'incertitude à l'aide d'un menu déroulant, sous le résultat.
Affichage du résultat
On peut afficher le résultat sous quatre formes différentes :
- Sans puissances de 10 (par ex.: 3.45 ± 0.12)
- Notation scientifique : (34.5 ± 1.2) · 10^-1
- Notation ingénieur : (3450 ± 120) · 10^-3
- Sans point décimal : (345 ± 12) · 10^-2
Autres
Le programme permet de :
- Enregistrer ou ouvrir une configuration (fichier .xml avec nom, formule, valeur et incertitudes) vers ou depuis le disque dur
- Placer des configurations dans un menu local (stocké sur l'ordinateur pour un navigateur donné)
- Transformer une configuration en url (pour être copiée dans un document pdf ou html)
- Utilisation de lettres grecques (bouton tout en haut à gauche) dans le champ de l'expression ou de la valeur d'une variable
- Dans le champ valeur d'une variable, on peut écrire une sous-formule comprenant des variables (nouvelles ou déjà utilisées). La variable sera alors remplacée par cette sous-formule. Par exemple, si une distance x possède la « valeur » : d km et que km est ensuite défini par 1000, on peut donner la valeur de d en kilomètres (mais x sera alors en mètres :-)
L. Schellenberg 3.2.2023