Expérimenter la gravitation universelle

Résumé

Cette animation permet de créer des astres en définissant leurs emplacements dans l'espace (à deux dimensions), leurs vitesses initiales et leurs masses, puis de les voir évoluer dans l'espace en les abandonnant à l'interaction gravitationnelle. Voici quelques activités qu'on peut proposer aux élèves (selon leur niveau, le temps à disposition et la matière traitée au cours :

• Juste s'amuser à voir comment évolue une certaine situation de départ
• Essayer d'obtenir une trajectoire circulaire d'une planète (masse = 1) autour d'une étoile (masse > 3000) en variant le vecteur vitesse initial
• Essayer de construire un système Soleil–Terre–Lune
• Vérifier les lois de Kepler (voir plus bas)
• Calculer la vitesse initiale pour qu'une planète décrive un cercle autour d'une étoile
• Calculer la vitesse de libération d'un petit astre par rapport à un grand et vérifier…

Prise en main

En essayant un peu tous les boutons au bas de l'écran, on doit pouvoir se faire une idée des possibilités de l'animation. Voici un petit tour d'horizon (ou du cosmos) dévoilant quelques facettes supplémentaires …

Création et modification du système d'astres

• Modifier la position d'un astre : amener la souris sur l'astre, puis, lorsque sa position (x, y)  s'affiche, cliquer-glisser…
• Modifier la masse d'un astre : amener la souris sur le bord de l'astre, puis, lorsque la masse s'affiche, cliquer-glisser vers l'intérieur ou vers l'extérieur de l'astre…
• Modifier la vitesse d'un astre : amener la souris sur l'extrémité de la flèche verte (vecteur vitesse) de l'astre, puis, lorsque la vitesse (vx, vy) [v] s'affiche, cliquer-glisser…
• Créer un nouvel astre : clicliquer (double-clic) sur le fond de l'écran…
• Supprimer un astre : clicliquer sur l'astre…
• En cliquant sur le bouton Edition, on peut effectuer les points ci-dessus et en plus demander de ne pas afficher la trajectoire de l'astre. On peut même y créer un astre avec une masse choisie aléatoirement et non affichée pour pouvoir la calculer (voir plus bas)

Commandes de la ligne 1

• Aide : Résumé succinct de la grande majorité des possibilités. Une aide plus explicite avec des conseils est prévue…
• Sauver : Enregistrer la configuration actuelle dans un fichier dans les téléchargements
• URL : Créer une url contenant la configuration actuelle : elle est copiée dans le presse-papier et peut ensuite être utilisée comme lien dans un document html ou pdf pour lancer l'animation directement avec cette configuration
• Ouvrir : Ouvrir un fichier .xml contenant une configuration précédemment sauvegardée
• SVG : Enregistrer une copie d'écran (sur fond blanc…) haute définition dans les téléchargements. Elle peut être incorporée dans une feuille Geogebra classic en ligne pour vérifier les lois de Kepler (voir plus bas).
• 🖨 (imprimante) : crée une image SVG (haute définition) qu'on peut alors imprimer (cmd-p ou ctrl-p) après avoir éventuellement modififé la taille des points ou l'épaisseur des traits à l'aide d'une petite fenêtre apparaissant sur l'écran…
• – (case à cocher) : si cochée, dessiner les orbites également avec un trait
• ↕ (case à cocher) : si cochée, adapte la zone d'impression aux trajectoires visibles 
• Start (Pause) : abandonne le système à la gravitation (ou le met en pause)
• Réinitialiser : remet le système dans le conditions initiales
• + : augmente la vitesse de l'animation (ips : images par seconde), mais sans changer (en principe) les trajectoires obtenues…
• - : diminue la vitesse de l'animation
• Enregistreur : une fois un système en pause (avec des trajectoires affichées), cette fenêtre permet de revenir en arrière, par bonds ou de manière continue ou d'avancer par bonds ou normalement…
• Edition : afficher la fenêtre d'édition des paramètres des astres. Les flèches en haut permettent de passer d'un astre à l'autre (qui se colore alors en bleu). Voir aussi sous fenêtre d'édition plus bas…
• ← : pour revenir en arrière dans l'historique des modifications du système (annuler…)
• → : défait la dernière annulation
• Univers : permet de voir la valeur de la constante universelle de la gravitation G de l'animation (différente de la valeur réelle) ainsi que le facteur de puissance de r dans la formule de la force gravitationnelle entre deux corps (pas très plausible, mais ça donne des résultats rigolos…)
• Français (menu local) : permet de choisir d'autres langues pour tous les textes et libellés de ll'animation

Commandes de la ligne 2

• Opacité : règle en bloc les opacités des diverses fenêtres de réglage (Aide, Sauver, Ouvrir, Enregistreur, Univers)
• Référentiel CM : place le système (ou plutôt l'écran) dans le référentiel du centre de masse du système
• Montrer la grille : affiche une grille de constante 100 px qui peut servir de repère pour rendre une orbite circulaire, par exemple…
• Fond blanc : ciel blanc et points de la trajectoire noirs, comme pour l'impression…
• Afficher les vitesses en mouvement : pour afficher les vecteur vitesse des astres lors de l'animation
• Afficher les trajectoires : affiche les trajectoires des astres dont la propriété Trajectoire est cochée, ou aucune si décochée…
• Un point sur dix (menu local) : le programme fait un nouveau calcul de la position 40 fois par seconde (mais on peut modifier ce nombre avec les boutons + et - ) ; ce menu permet de choisir (pour toutes les trajectoires) la fraction des points calculés qui doit être affichée à l'écran

Fenêtre d'édition

• Accessible par le bouton Edition ou en cliquant sur un astre
• On peut créer une masse aléatoire dont la valeur est cachée (bouton ?, en bas de la fenêtre). Pour la rendre visible, cliquer sur le bouton 🔓 (cadenas ouvert) qui se trouve sur la ligne masse, tout à droite. Pour la recacher, cliquer sur le bouton 🔒 (cadenas fermé)…

Informations sur l'écran

• Coin supérieur droit : nombre d'images par seconde (arrondi à l'entier le plus proche)
• Coin inférieur droit : temps de l'animation (utilisé dans les calculs) depuis le début (et nombre d'instantannés mémorisés)
• Coin inférieur gauche : état de l'animation (Edition ou rien…)

Réalité physique

L'animation utilise une simple méthode d'Euler pour calculer l'évolution du système (pour une position donnée, on calcule la résultante des forces gravitationnelles agissant sur chaque astre, on en tire l'accélération de l'astre et on calcule le nouveau vecteur vitesse v' = v + a·dt et le nouveau vecteur position r' = r + v·dt, après un temps dt, puis on recommence… Cette opération est effectuée 10 fois pour chaque position enregistrée, pour augmenter la précision. En cas de collision de deux astres, les deux fusionnent et continuent dans la direction de leur vecteur quantité de mouvement total…

Les unités affichées sont évidemment arbitraires (positions, vitesses, masses, temps écoulé et constante universelle de la gravitation G), mais on peut faire comme si c'étaient des mètres, des mètres par seconde, des kilogrammes, des secondes et G en mètres-cube par kg·secondes-carré).

Le temps affiché dans le coin inférieur droit (en mode animation normal, en pause ou en replay), est le temps pendant lequel le système a évolué depuis le départ de l'animation (Réinitialisation, puis Start) et peut donc être utilisé pour déterminer des périodes (temps pour un tour). C'est ce temps-là qu'il faut utiliser dans les calculs et il est plus fiable que le temps chronométré par un chronomètre qui, lui, est faux car l'ordinateur partage des tâches externes pendant l'animation et à cause d'imprécisions internes. 

Activités

Ludiques pour explorer…​

• Créer (en tâtonnant) un système Terre–Lune où la Lune décrit un cercle parfait
• Créer un système Soleil-Terre-Lune (masses par ex. : 10'000, 100, 1)
• Créer un système d'étoiles binaires (deux étoiles qui tournent autour d'un même point)
• Idem, mais en plus une planète qui leur tourne autour…
• Idem avec trois astres qui tournent autour d'un même point
• …

Démonstations

En appuyant sur la touche ? du clavier (ou ±), on peut afficher un petit menu avec des configurations particulières…

L'animation respecte-t-elle la première loi de Kepler ?

Il s'agit de vérifier la phrase suivante :

L'orbite d'une planète autour d'une étoile est une ellipse et l'étoile occupe l'un des foyers de l'ellipse

Pour que cela fonctionne, il faut que la petite masse soit vraiment beaucoup plus petite (masse 1) que la grande (masse 5000), sinon la grande ne resterait pas immobile.

Vérifier que l'orbite est une ellipse, c'est vérifier la propriété que la somme des distances d'un point de l'ellipse aux deux foyers est constante.

Avant de vérifier si l'animation respecte cette première loi de Kepler, il faut donc commencer par construire le second foyer (situé de manière symétrique au premier, par rapport au centre de l'ellipse). Voici une animation Geogebra qui montre comment construire le grand axe de l'ellipse, le centre et le second foyer.

Une fois construit le second foyer, il faut vérifier que l'orbite possède bien la propriété de l'ellipse mentionnée ci-dessus . Démarche pour la premier loi de Kepler

Et la deuxième loi de Kepler ?

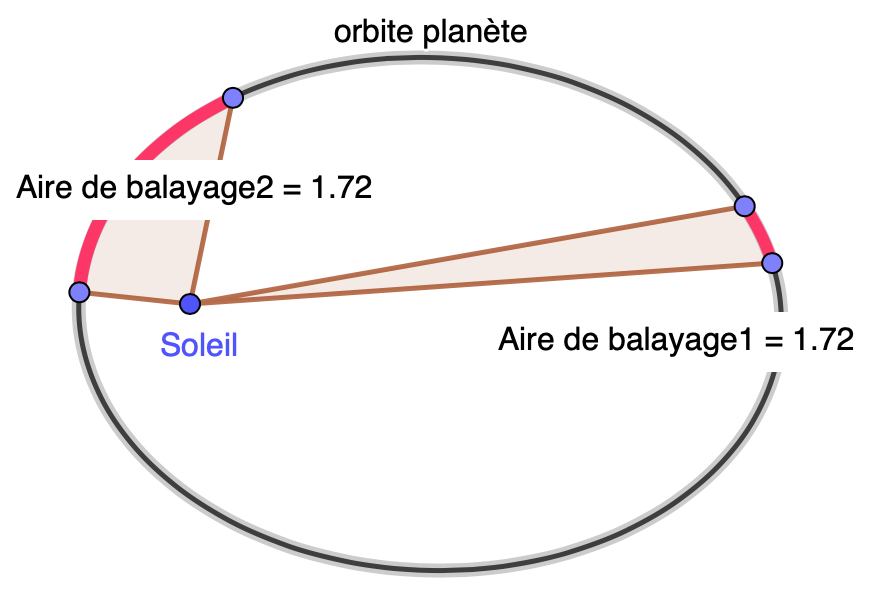
Chaque planète balaye des aires égales en des temps égaux

Dans le schéma ci-dessous, on voit une orbite planétaire très excentrée. Quand la planète passe du point tout à droite à celui qui est juste à côté, l'aire balayée par la planète (surface saumon) est 1.72. Quand la planète va du prochain point à celui qui est tout à gauche, l'aire balayée est la même, mais le chemin parcouru est bien plus grand. D'après la deuxième loi de Kepler les temps nécessaires pour balayer chacune des deux surfaces sont égaux. Cela implique notamment que la planète se déplace plus rapidement à gauche qu'à droite. Ou encore que la vitesse de la planète augmente au fur et à mesure qu'elle se rapproche de l'étoile (Soleil)…

Voici la marche à suivre pour se convaincre que l'animation respecte la deuxième loi de Kepler

Et la troisième loi de Kepler ?

Pour chaque planète d'un système planétaire, si on divise le carré de la période T (temps pour un tour) par le cube du demi grand axe a (rayon moyen ou distance moyenne entre l'étoile et la planète au cours d'un tour), on obtient toujours le même nombre, la constante de Kepler K :

                              

Pour vérifier si l'animation respecte la troisième loi de Kepler, il faut créer une étoile (masse : 5000) et deux planètes (masses : 1) et les placer à deux endroits différents de l'étoile, pas à la même distance de celle-ci. Il s'agit de choisir les vitesses initiales de manière à ce que le rapport des grands axes des deux trajectoires obtenues soit d'environ 1.3 (il faut donc faire des essais…). Pour l'analyse, il faudrait que les deux planètes bouclent au moins 70% d'un tour et moins d'un tour complet. Voici la marche à suivre pour la vérification de la troisième loi de Kepler.

Remarques :

• Les unités utilisées ne sont pas importantes, mais il faut utiliser le mêmes pour chaque trajectoire !
• Comme la construction commence par la construction des deux grands axes, on peut gagner passablement de temps en choisissant pour chaque planète une vitesse initiale perpendiculaire aux rayon étoile–planète. En effet, dans ce cas, le point de départ se trouve forcément sur le grand axe et il suffit donc de mener une droite par ce point initial et par l'étoile pour avoir le grand axe !
• Plutôt que de déterminer la période (ou un nombre proportionnel à la période), on pourrait simplement chronométrer le temps pour un tour pour chacune des deux planètes et remplacer T par ce temps…

Calculs avec la formule pour la vitesse de satellisation

• On peut utiliser la formule pour la vitesse que doit avoir une planète pour décrire un cercle de rayon r autour d'un astre de masse M (vitesse de satellisation) :

On peut donc calculer cette vitesse (attention, prendre le G de l'animation qui vaut 100 par défaut), puis régler la vitesse de la planète avec le résultat du calcul et appuyer sur Start pour voir le résultat.

• Inversement, on peut varier la vitesse initiale jusqu'à obtenir une orbite parfaitement circulaire (afficher la grille !), puis déterminer la valeur de G et vérifier avec le bouton Univers…
• Ou encore déterminer la masse M d'une étoile (pour cela, afficher la fenêtre d'édition avec le bouton Edition, puis créer un astre dont la masse est cachée (et de valeur aléatoire) en cliquant sur le bouton ? (point d'interrogation, en bas de la fenêtre)
• Sachant que la constante de Kepler vaut également

 (a est le demi grand axe) on peut aussi trouver G (ou M, si M est caché…) avec une orbite elliptique dont on détermine le demi grand axe…

• On peut aussi essayer de prévoir les vitesses à donner à deux étoiles ayant la même masse (ou différentes, ce qui complique un peu les équations) pour qu'elles décrivent des cercles autour du centre de masse commun

L. Schellenberg, le 16.2.2023